Hello Radio: How to Listen to FM Radio Using LimeSDR

LimeSDR is an open source software defined radio which can support a continuous frequency range from 100KHz to 3.8GHz. Many wireless systems such as 2/3/4G, Wifi and FM radio are covered in this frequency range, which makes LimeSDR a fairly useful tool.

To test a software defined radio, usually the first experiment to run is to listen to FM radio. FM radio is the equivalent of Hello World in the universe of the software defined radio. Before starting to describe how to run FM radio test, we have a list of HW/SW needed:

1. LimeSDR board with antenna connected

2. FM transmitter which pairs with a smart phone

3. Lime Suite GUI (version 20.10.0)

4. GNU Radio (version 3.7.11)

The test is done using Ubuntu 18.04.4 LTS.

Step 1: LimeSDR configuration file generation

In the test, we will listen to a FM radio channel set at 89.0MHz. Therefore, LimeSDR needs to generate a tone at 89.0MHz, multiply this tone with the input radio signal, and down-convert the ratio signal to the baseband for further processing. To generate this configuration, in Lime Suite GUI -> SXR, Freq needs to be set as 89.0MHz, then calculate and tune. By pressing the "Save" button at the top left of the GUI, the configuration file will be save as fm_receiver_89Mhz.ini for future usage.

Step 2: GNU Radio set up

GNU Radio is a popular tool for software define radio. To make GNU Radio work together with LimeSDR, one needs to install both GNU Radio and gr-limesdr, a LimeSDR library for GNU Radio. After that, FM_receiver.grc file from /gr-limesdr/examples folder can be loaded into GNU Radio. A few changes need to be made before starting to run it. First, device serial #, .ini file and RF Frequency need to be modified in the LimeSuite Source (RX) module. Device serial # is the serial number for the LimeSDR device and it can be read from Lime Suite GUI; The .ini LimeSDR configuration file has been generated in step 1; RF freq is to be set as 89.0MHz. Baseband Freq in the WX GUI FFT Sink module also needs to be updated to 89.0MHz. Then by pressing the green triangle "Execute the flow graph" button, GNU Radio starts to run. 

Step 3: Run Test

However, you often only hear noise even if the frequency tuned to is a valid local radio channel. The issue is likely due to antenna setting. A rule of thumb is that the antenna size should be in similar dimension as the wavelength of the wireless signal received. For FM radio at 89.0MHz frequency, the wavelength is 300,000,000/89,000,000 = 3.37 meter. But the antenna bought together with LimeSDR is only 4.5 cm long. The antenna size is too small for FM radio. Based on the antenna length, it is designed for multi-GHz freq signal instead of for FM radio which ranges from 88MHz to 108MHz. There are at least two ways to fix it. The first way is to use a different antenna which is much longer. The second way is to move LimeSDR closer, much closer, to the radio transmitter or the other way around. We use the second way. We bought a FM transmitter which can be plugged into the smart phone and tune it into 89.MHz. Then by putting FW transmitter almost right next to the receiver antenna (shown in the second photo below, the first photo shows the my LimeSDR/antenna and their Lego housing), we can now hear the music. 

Task accomplished!

Signal Processing Magic (7) -- Doppler Shift, Rayleigh fading and Jakes model

Doppler shift was discovered by a physicist named Christian Doppler long time ago. Doppler shift is used to characterize the frequency change due to movement. A typical example is that when a fire truck drives toward you, the tone of its siren changes over the time because its speed towards you varies.

Doppler shift for wireless communication is

\[f_d=v/c*f_c\]

whereas v is the speed of the object, c is the speed of light, and \(f_c\) is carrier frequency. For instance, if you sit on a high-speed training moving at 350km/h browsing Internet and your phone is using a 3GHz band, then 

\[f_d = (350*1000/3600)/(3*10e8)*3*10e9 = 972 Hz\]

Based on this equation, moving faster as well as using a band with higher carrier frequency will make Doppler shift larger. Usually the highest Doppler shift is observed in high-speed train. Larger Doppler shift makes channel estimation harder in wireless communication.

Rayleigh fading is a commonly used model for a wireless channel, and it is used when the transmitter can't see the receiver such as in Manhattan island. Rayleigh fading model can be derived from joint Gaussian distribution. Assuming \(x\) and \(y\) are two zero-mean Gaussian R.V. orthogonal to each other, their joint distribution becomes:

\[f_{X,Y}(x,y)=\frac{1}{2\pi\sigma^{2}}e^{-\frac{x^2+y^2}{2\sigma^2}}\]

Rayleigh fading tracks the envelope, \(r\). With \(r^2=x^2+y^2\), we have \(x=r*cos(\theta)\) and \(y=r*sin(\theta)\). To transfer a \(f_{X,Y}(x,y)\) to distribution of \(r\), the determinant of the Jacobian matrix needs to be found:

\[J(r,\theta)=det\begin{bmatrix}\frac{\partial x}{\partial r}&\frac{\partial x}{\partial \theta}\\\frac{\partial y}{\partial r}&\frac{\partial y}{\partial \theta}\end{bmatrix}=det\begin{bmatrix}cos(\theta)&-r*sin(\theta)\\sin(\theta)&r*cos(\theta)\end{bmatrix}=r\]

Therefore,

\[f_{R,\Theta}(r,\theta)=\frac{J(r,\theta)}{2\pi\sigma^{2}}e^{-\frac{r^2}{2\sigma^2}}=\frac{r}{2\pi\sigma^{2}}e^{-\frac{r^2}{2\sigma^2}}\]

After integrating over \(2\pi\) to remove \(\theta\), Rayleigh fading model is:

\[f_{R}(r)=\frac{r}{\sigma^{2}}e^{-\frac{r^2}{2\sigma^2}}\] 

for \(r\geq0\).

In reality, fading channel is always correlated in time. That means the wireless channels your phone sees in this moment and the next moment are always more or less similar. Fourier transmission of wireless channel's time-domain auto-correlation becomes its Power Spectral Density (PSD). For Rayleigh fading with vertical antenna and signal coming from all angles in uniform distribution, it has a famous PSD called Jakes model. Jakes model also depends on Doppler shift, and it is:

\[S(f)=\frac{1}{\pi f_d}\frac{1}{\sqrt{1-(f/f_d)^2}}\]

when \(|f|\leq f_d\) and \(S(f)=0\) otherwise. Jakes model has a famous U shape and the width of the "U" depends on Doppler shift, \(f_d\). When \(f_d=0\), Jakes model is an impulse and it means Rayleigh channel never changes.

Low Light Image Combining Using Python (3) -- Running Even Faster

In this blog, we will discuss how to make lower light image combining run even faster. 

Image alignment is the most time-consuming stage of low light image combining. By using a method similar to what has been proposed in HDR+ project page (https://www.timothybrooks.com/tech/hdr-plus/), we introduce decimation to image alignment and it brings big saving in calculation time.

This is how decimation helps: as discussed earlier, assume block size is B, search range in both horizontal and vertical S, the complexity of image alignment is proportional to B*S*S. For a 4k x 3k image and search range equal to 40 ([-40,40] with each even position), the complexity for matching each pair is 19.2G operations, which is enormous. To save MIPS, we can divide this process to two steps:

Step 1: decimate the image by 16. After decimation, it becomes much easier to align images with the cost of reduced accuracy. The complexity of step 1 now becomes B/16*S*S.

Step 2: we are not done yet. Decimating the original image by 16 means aggregating 16 pixels of the original pixel to one. Now it is time to find out exactly which one of these 16 pixels provides the best alignment so that there is no sacrifice on accuracy. But the search range is drastically reduced. We now align with original image with size B but less range with new S' = 4. S' = 4 is sufficient to find one out of 16 pixel candidates.

Breaking the original image alignment to two steps reduces MIPS quite a bit: instead of B*S*S = 19.2G, now we have B/16*S*S + B*4*4 = 1.39G, a reduction of 93% of complexity. 

By our experiment, the new execution time of the whole image combining process becomes 9.7s without any help from multicore, which is a roughly 1/4 of the baseline. The sample code can be found here: https://github.com/legendzhangn/blog/tree/master/lowlight_image_combine_even_faster

Low Light Image Combining Using Python (2) -- Running Faster

In a previous blog, a Python script to combine several low light raw images for improved SNR has been introduced. But that script runs rather slow. To combine four images together, it takes 155.8s in my PC which uses Intel i5-8400 @ 2.8GHz x 6 core with 16GB memory. How to run it faster? After some attempts, we are able to cut the time to roughly 1/8 of the baseline mainly with two tricks: 1) using decimated image for alignment; 2) processing in multi-core. The new processing times are:

Baseline: 155.8s
After using decimated image for alignment: 40.6s
After using decimated image for alignment + processing in multi-core: 21.1s

Now let me show you how to do it:

Using decimated image for alignment

Image alignment is the most computationally intensive part of the image combining pipeline. In fact, the time spent on image alignment is more than 90% of the total. The operation of image alignment is shown below. During image alignment, the candidate block is swiped though the target block in both horizontal and vertical directions. Assume block size is B, search range in both horizontal and vertical are S, the complexity of image alignment is proportional to B*S*S. For a 4k x 3k image and search range equal to 40 ([-40,40] with each even position), the complexity for matching each pair is 19.2G operations, which is enormous.

One observation is that due to the structure of Bayer pattern, we only calculate candidate of even number of pixel shift such as 0/2/4 etc. Then a natural thought is to decimate both candidate and target by 2. This will bring ~4x acceleration. Instead of B*S*S complexity, it is now B*S*S/4. This explains why processing time is reduced from 155.8s to 40.6s after decimation. Performance wise, this decimation means that instead of using pixels of all colors, only one out of four pixels with green color will be used for alignment. However, the quality of combining seems to hold, which indicate that there are enough pixels left to guarantee the quality of image alignment. The Python code change is below, ":2" is the delta:

Old code:

candidate = rgb_raw_image_candi[f,row_start+row_offset+boundary_adjust[row, col, 0]:row_end+row_offset+boundary_adjust[row, col, 1],
col_start+col_offset+boundary_adjust[row, col, 2]:col_end+col_offset+boundary_adjust[row, col, 3]]
target = rgb_raw_image[row_start+boundary_adjust[row, col, 0]:row_end+boundary_adjust[row, col, 1],
col_start+boundary_adjust[row, col, 2]:col_end+boundary_adjust[row, col, 3]]

New code:

candidate = rgb_raw_image_candi[row_start+row_offset+boundary_adjust[row, col, 0]:row_end+row_offset+boundary_adjust[row, col, 1]:2,
col_start+col_offset+boundary_adjust[row, col, 2]:col_end+col_offset+boundary_adjust[row, col, 3]:2]
target = rgb_raw_image[row_start+boundary_adjust[row, col, 0]:row_end+boundary_adjust[row, col, 1]:2,
col_start+boundary_adjust[row, col, 2]:col_end+boundary_adjust[row, col, 3]:2]

Multi-core processing

Our baseline script use single thread to process. By distributing tasks to multiple threads, we expect the running time to be shorter. Introduction of Python-based parallel processing can be found here. Our task is to align three images with the base image. Therefore, it can be divided into three sub-tasks which are to align each image with the base. In this way, these three sub-tasks can be run independently which brings the best parallel processing gain. Since the sub-tasks are independent, we use the most basic parallel processing module of pooling. What pooling module does is to assign each sub-task to a thread. image_align is the function for sub-task execution and image_input is a list with each element to be input images for a sub-task.

Pooling code:

with Pool(6) as p:
    image_output = p.map(image_align, image_input)

Due to the overhead of parallel processing, the processing time is not cut to 1/3 of single thread. However, parallel processing does reduce the running time by ~20s (40.6s -> 21.1s). In general, when each sub-task is more computationally heavier, there is more time saving by parallel processing.

With both alignment with decimated image and multi-core processing, the final processing time is reduced to 21.1s from 155.8s. My code can be found here 

Low Light Image Combining Using Python (1)

Low light images are photos taken while it is dark. Low light images are usually noisy since there is not enough light coming in. To reduce the noise, a commonly used way is to combine multiple images. For example, such a method has been used in Google pixel camera night mode. Here we will show a Python script which does simple low light image combining.

The pipeline includes three steps: raw image alignment, raw image combining, post processing.

Raw image is the direct output of the image sensor. In normal photo, each pixel has three color channels as R/G/B. But in raw image, each pixel only has one color channel. Bayer pattern is widely used in raw image, and it is also used in this experiment. The color pattern used here is shown below which is one kind of Bayer patterns. As one can see, out of 24 pixels, half of them are green, 25% is red and 25% is blue. The reason that green channel occupies the most pixels is because human eye is the most sensitive to green color.

   0 1 2 3 4 5
0 G R G R G R
1 B G B G B G
2 G R G R G R
3 B G B G B G

What raw image alignment does is to align two raw images. Since multiple images are taken at different times, due to hand movement, there will be small shift of the image. Without alignment, adding images together will create blurry photo. Our method for image alignment is straightforward. To align two images, we will divide both images to blocks with equal dimension. By calling one image "target" and the other image "candidate", we will swipe the candidate block through the target block in both x and y axis search directions. The scope of the swipe is called search range. For each swipe position, the L1 distance will be calculated which is the delta of the pixel values of the candidate and target blocks. Out of all swipe positions, the one with smallest L1 distance will be selected. For more details of this operation, you can refer to the Python source code here.

The reason that image alignment should be done at the very beginning of the image pipeline on raw image is for both performance and computation time. In term of performance, additional processing of the signal at the later stages such as interpolation/correlation may degrade the performance of alignment. In term of computation time, raw image has one color in a pixel but at later stages after interpolation, there will be three colors in each pixel. Calculating alignment on one color channel is faster than calculating that on three channels. Due to the structure of Bayer pattern, we only calculate candidate of even number of pixel shift such as 0/2/4 etc.

The step of raw image combining is to add candidate and target blocks together. Since they are already aligned, adding them together will enhance the signal while reducing the noise. Here we apply equal weight to each image. However, performance could be improved by applying different weights.

Between raw image and the photo we usually see, post processing needs to be done. Libraw library is used for post processing. The major steps of post processing is shown below:

Next we will show the outcome of combining. Raw images are obtained using Pro camera mode of a Samsung Galaxy S9 device. The camera settings are ISO = 800, 1/4 shutter speed, and F1.5. S9 has two aperture modes: F2.4 and F.15. F1.5 is a larger aperture for low light photo. Figure below shows the difference before (left) and after (right) the combining. The image quality is clearly improved. To get the right figure, we combine eight low light images. Bilateral filtering can be used to further enhance the image quality.

Source code of the Python script and raw image files can be found here: https://github.com/legendzhangn/blog/tree/master/lowlight_image_combine

LibRaw Post Processing Pipeline Translated Into Python (2) -- Low Light Photo

In a previous post, we introduced a Python script which emulates the pipeline of LibRaw. LibRaw is a commonly used library for raw image conversion.

Then we found that compared with LibRaw, our Python script does not work well for raw image taken under low light. While LibRaw still shows the objects albeit quite noisy, our original Python script does not show anything. After some digging, it is found that LibRaw has an auto bright function which is not available in the previous Python script. As shown below, for low light image, the difference made by using auto bright function is quite stark.




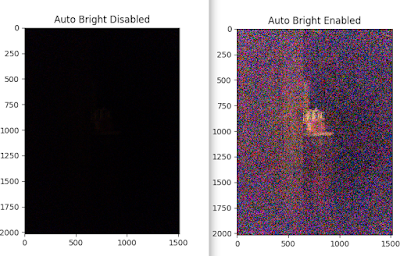
Thereafter, our Python script gets updated and now it supports auto bright as well. The main difference between low light image and normal light image is how Gamma mapping is done. For low light image, Gamma curve peaks much faster than for normal light image. The exact Gamma curve of low light image depends on its histogram. The updated script can be found here, and it shows how this new Gamma curve is generated.